Fundamentos de cartografía y geodesia¶
Trabajo previo¶
Lecturas¶
Olaya, V. (2020). Sistemas de Información Geográfica. https://volaya.github.io/libro-sig/ (Parte 1, capítulo “Fundamentos cartográficos y geodésicos”)
Resumen¶
La cartografía es el estudio y la práctica de hacer y estudiar mapas. En este capítulo se detallan los principales conceptos cartográficos y geodésicos requeridos para el trabajo con datos geoespaciales.
Conceptos geodésicos básicos¶
La geodesia es la ciencia que trata de la medición de la forma de la Tierra, su orientación en el espacio y su campo gravitacional. Entre las tareas típicas de un geodesta están, por ejemplo, la delineación de costas, el establecimiento de límites de entidades territoriales administrativas (ej. países, provincias) y la medición de áreas de territorios.
El planeta Tierra tiene forma esférica, sin embargo, no es una esfera perfecta: es achatada en los polos y abultada en el Ecuador. Además, su superficie es irregular debido a accidentes geográficos como valles, montañas o depresiones tectónicas, entre muchos otros.
Para realizar sus cálculos y mediciones, los geodestas deben utilizar varios modelos matemáticos, los cuales aproximan la forma real de la Tierra. Entre estos modelos están el elipsoide de referencia y el geoide. Las características de estos modelos pueden variar para satisfacer requerimientos particulares de navegación, agrimensura, catastro, uso del suelo y otras cuestiones de interés. Con estos modelos, uno de los objetivos principales de la geodesia es establecer un sistema de referencia y definir un conjunto de puntos (conocidos como vértices geodésicos ) cuyas coordenadas en dicho sistema sean conocidas con una precisión elevada. Posteriormente, y en base a esos puntos, los cuales forman una red geodésica, se pueden calcular las coordenadas de cualquier punto en el sistema de referencia definido [Ola20].
Elipsoide de referencia¶
El elipsoide de referencia es el modelo más sencillo de la forma de la Tierra. Se define por dos parámetros: el radio ecuatorial (semieje mayor) y el radio polar (semieje menor), los cuales se ejemplifican en la Fig. 3.
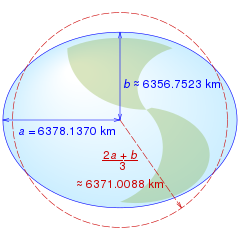
Fig. 3 Radio ecuatorial y radio polar del elipsoide de referencia del sistema geodésico WGS84. Imagen de Cmglee compartida a través de Wikimedia Commons.¶
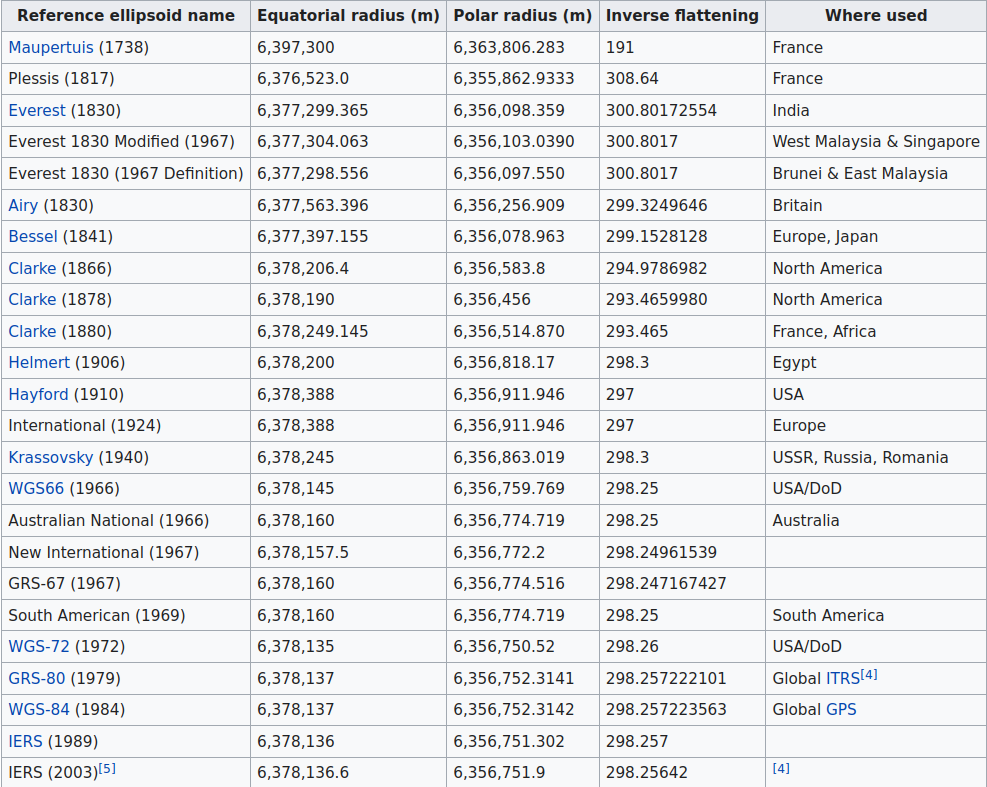
A través de la historia, se han utilizado diferentes elipsoides cuyas medidas varían de acuerdo con los instrumentos y conocimientos disponibles en cada época y lugar. La lista de la Fig. 4 muestra algunos de estos elipsoides de referencia y sus parámetros.
Los primeros elipsoides de referencia fueron diseñados para usos locales (ej. Europa, India, América del Norte). Más recientemente, se identificó la necesidad de contar con modelos para todo el planeta, como el del elipsoide WGS84, uno de los más utilizados en la actualidad, por ser el empleado por el Sistema de Posicionamiento Global (GPS; en inglés, Global Positioning System). El WGS84 (World Geodetic System 1984) es la revisión más reciente del World Geodetic System (WGS), un estándar mundial usado en geodesia, cartografía y navegación.
Geoide¶
El elipsoide tiene una superficie lisa y no puede representar las protuberancias y depresiones de la Tierra. El geoide es un modelo mucho más acertado de la superficie del planeta que sí contempla estas características. La Fig. 5 muestra una imagen de un geoide.
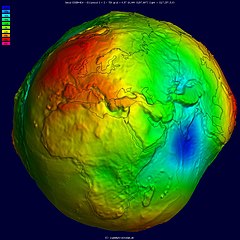
Fig. 5 Geoide. Imagen de ICGEM compartida a través de Wikimedia Commons.¶
De manera similar al caso de los elipsoides, existen varios geoides de referencia que han sido desarrollados a través del tiempo y han evolucionado para adaptarse a las modificaciones de la superficie terrestre.
Datum geodésico¶
Cuando se trabaja con un elipsoide global (ej. WGS84), se sitúa de tal modo que tanto la posición de su centro de gravedad como su plano ecuatorial coincidan con los terrestres. Por el contrario, cuando el elipsoide es local, estas propiedades no se cumplen necesariamente, y el elipsoide resulta insuficiente, ya que no se cuenta con información sobre su posicionamiento con respecto a la superficie terrestre [Ola20].
Surge así el concepto de datum, que es el conjunto formado por una superficie de referencia (el elipsoide) y un punto en el que este se une al geoide. Este punto se denomina punto astronómico fundamental (para su cálculo se emplean métodos astronómicos), o simplemente punto fundamental, y en él el elipsoide es tangente al geoide [Ola20].
Para un mismo elipsoide pueden utilizarse distintos puntos fundamentales, que darán lugar a distintos datum y a distintas coordenadas para un mismo punto [Ola20]. Además de los datum globales o continentales, varios países han creado sus propios datum para hacer su cartografía lo más precisa posible. Algunos de los datum usados en la actualidad son:
WGS84: para todo el mundo.
NAD27 (North American Datum 1927) y NAD83 (North American Datum 1983): para América del Norte.
ETRS89 (European Terrestrial Reference System 1989): para Europa.
ED50 (European Datum 1950) y ED79 (European Datum 1979): para España.
SAD69 (South American Datum 1969): para Brasil.
CR05 (Costa Rica 2005): para Costa Rica, declarado como datum oficial mediante Decreto Ejecutivo No. 33797-MJ-MOPT - PGR.
Sistemas de coordenadas¶
Una vez que se dispone de modelos precisos para representar la forma de la Tierra, es posible establecer un sistema para codificar cada una de las posiciones sobre su superficie y asignar a estas las coordenadas correspondientes. Así, podemos definir un sistema de coordenadas esféricas para un elipsoide. A este tipo de coordenadas se les llama coordenadas geográficas.
Por otra parte, muchas veces es útil situar los elementos de la superficie del elipsoide sobre una superficie plana, dando lugar a las proyecciones cartográficas, las cuales utilizan coordenadas cartesianas, también llamadas coordenadas planas, debido a que resultan de proyectar la superficie del elipsoide sobre un plano.
Coordenadas geográficas¶
El sistema de coordenadas geográficas es un sistema de coordenadas esféricas mediante el cual un punto se localiza con dos valores angulares denominados latitud y longitud, los cuales se muestran en la Fig. 6.
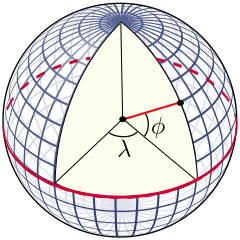
Fig. 6 Latitud y longitud en una esfera con una gratícula con intervalos de 10°. Imagen de Peter Mercator compartida a través de Wikimedia Commons.¶
La latitud (φ, o phi) de un punto en la superficie de la Tierra es el ángulo entre el plano ecuatorial y la línea que pasa por este punto y el centro de la Tierra. Todos los puntos con la misma latitud forman un plano paralelo al plano del ecuador. El ecuador es el paralelo 0° y divide el globo en hemisferios norte y sur; así el polo norte es 90° N y el polo sur es 90° S. A medida que la latitud aumenta, hacia el Norte o hacia el Sur, disminuyen los kilómetros por grado. Para el paralelo del Ecuador, sabiendo que la circunferencia que corresponde al Ecuador mide 40 075,017 km, 1° equivale a 111,319 km (resultado de dividir el perímetro del ecuador entre los 360° de longitud).
La longitud (λ, o lambda) de un punto en la superficie de la Tierra es el ángulo entre el meridiano de referencia y el meridiano que pasa por este punto. El meridiano de referencia mayormente aceptado es el meridiano que pasa por el Real Observatorio de Greenwich, situado al sureste de Londres, Inglaterra. Este primer meridiano determina los hemisferios este y oeste. Las líneas de longitud forman semicírculos máximos que pasan por los polos y se llaman meridianos. La distancia en km a la que equivale un grado de longitud depende de la latitud.
Las líneas de los paralelos y meridianos se ilustran en la Fig. 7.
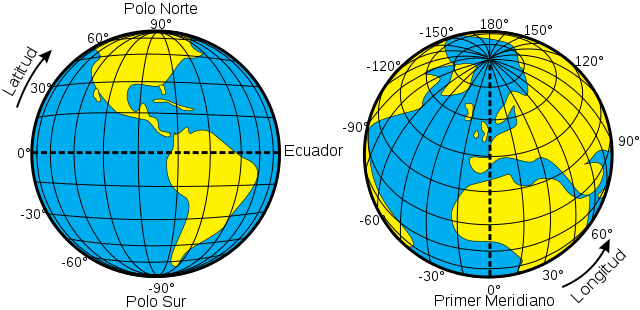
Fig. 7 Paralelos y meridianos. Imagen de Djexplo compartida a través de Wikimedia Commons.¶
Las coordenadas geográficas resultan de gran utilidad, especialmente cuando se trabaja con grandes regiones o con sitios distribuidos por todo el planeta. Sin embargo, no se trata de un sistema cartesiano, y tareas como la medición de áreas o distancias es mucho más complicadas. Si bien la distancia entre dos paralelos es prácticamente constante (es decir, un grado de latitud equivale más o menos a una misma distancia en todos los puntos), la distancia entre dos meridianos no lo es, y varía entre unos 11,3 kilómetros en el Ecuador hasta los cero kilómetros en los polos, donde los meridianos convergen [Ola20].
Proyecciones cartográficas¶
En muchas situaciones, los sistemas cartesianos resultan más convenientes que los esféricos. En un sistema cartesiano, la posición de un punto se define mediante un par de medidas de distancia: x e y. Además, las representaciones visuales de la información cartográfica son más cómodas de manejar en una superficie plana (ej. una lámina de papel o la pantalla de una computadora) que en una esférica (ej. un globo terráqueo).
El resultado de asignar una coordenada plana a cada punto de la superficie de la Tierra (que no es plana) se conoce como proyección cartográfica. Matemáticamente, se trata de asignar a cada par de coordenadas geográficas (longitud, latitud) un par de coordenadas cartesianas (x, y).
Tipos de proyecciones¶
Las proyecciones pueden clasificarse, según la superficie sobre la que se proyectan los objetos, en cilíndricas, cónicas y azimutales.
Cilíndricas: El globo terrestre se proyecta en una superficie cilíndrica. Son muy utilizadas, pero con frecuencia se modifican debido a las grandes distorsiones que muestran en las zonas de latitud elevada, lo que impide apreciar a las regiones polares en su verdadera proporción. Son muy útiles para apreciar la superficie de la Tierra completa, por lo que se utiliza en mapamundis. La Fig. 8 muestra un esquema de una proyección cilíndrica.

Fig. 8 Esquema de proyección cilíndrica. Imagen de Traroth compartida a través de Wikimedia Commons.¶
Cónicas: El globo terrestre se proyecta en una superficie cónica tangente, situando el vértice en el eje que une los dos polos. Aunque las formas presentadas son de los polos, los cartógrafos utilizan este tipo de proyección para ver los países y continentes. La Fig. 9 muestra un esquema de una proyección cilíndrica.

Fig. 9 Esquema de proyección cónica. Imagen de Traroth compartida a través de Wikimedia Commons.¶
Azimutales: También son llamadas proyecciones polares. Se proyecta una porción de la Tierra sobre un plano tangente al globo en un punto seleccionado, obteniéndose una imagen similar a la visión de la Tierra desde un punto interior o exterior. Se utilizan principalmente para los polos y los hemisferios. La Fig. 10 muestra un esquema de una proyección azimutal.
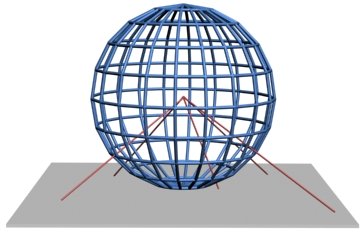
Fig. 10 Esquema de proyección azimutal. Imagen de Traroth compartida a través de Wikimedia Commons.¶
Otra forma de clasificar las proyecciones es según las propiedades métricas que conserven. Toda proyección implica alguna distorsión en las áreas, formas o distancias, como se muestra en la Fig. 11.
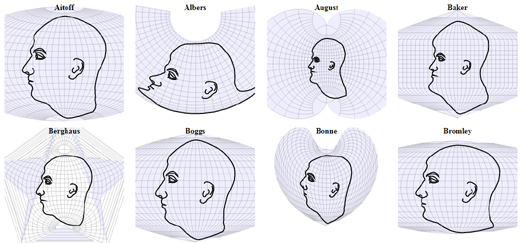
Fig. 11 Distorsiones en proyecciones cartográficas. Imagen de Jim Vallandingham compartida a través de bl.ocks.org (clic para ver la imagen completa).¶
De acuerdo con el criterio de la conservación de propiedades métricas, las proyecciones cartográficas pueden clasificarse en:
Equidistantes: si conservan las distancias.
Equivalentes (o equiáreas): si conservan las áreas.
Conformes: si conservan las formas (o, lo que es lo mismo, los ángulos).
No es posible conservar todas las propiedades a la vez, por lo que es necesario decidir cuales pueden perderse, de acuerdo con el uso que quiera dársele al mapa.
Ejemplos de proyecciones¶
Mercator¶
La proyección de Mercator fue creada por el cartógrafo flamenco Gerardus Mercator en 1569. Ha sido muy utilizada desde el siglo XVIII para cartas náuticas porque permitía trazar las rutas de rumbo constante como líneas rectas e ininterrumpidas, a diferencia de otras proyecciones más precisas. La proyección de Mercator se muestra en la Fig. 12.
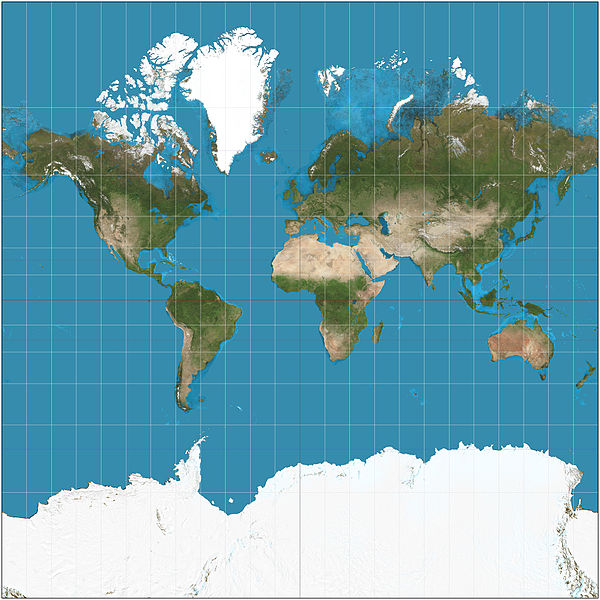
Fig. 12 Proyección de Mercator. Imagen de Strebe compartida a través de Wikimedia Commons.¶
Es un tipo de proyección cilíndrica tangente al ecuador. Como tal, deforma las distancias entre los meridianos en líneas paralelas, aumentando su ancho real cada vez más a medida que se acerca a los polos. Esta proyección tampoco respeta las formas reales entre los paralelos, la amplía en largo, cada vez más a medida que se acerca a los polos, distorsionando las áreas cercanas a los polos aún más.
La proyección de Mercator va exagerando el tamaño de las tierras a medida que nos alejamos de la línea del ecuador. Algunas de las distorsiones más conocidas que presenta son:
Groenlandia aparece aproximadamente del tamaño de África, cuando en realidad la superficie de África es aproximadamente 14 veces la de Groenlandia.
Alaska aparece similar en tamaño a Brasil, cuando el área de Brasil es casi cinco veces más grande que Alaska.
La Antártida parece ser extremadamente grande. Si se cartografiara todo el globo, la Antártida se inflaría infinitamente. En realidad, es el tercer continente más pequeño.
África parece tener aproximadamente el mismo tamaño que América del Sur, cuando en realidad África es más de una vez y media más grande.
El aumento de tamaño del norte también distorsiona mucho la forma de Rusia, haciéndola parecer mucho más alta de norte a sur y estirando mucho sus regiones árticas en comparación con sus latitudes medias.
Las diferencias entre el tamaño real de los países y territorios y su representación en la proyección de Mercator se muestra en varios sitios en la Web, entre ellos https://brilliantmaps.com/mercator-vs-true-size/ y https://mathigon.org/course/circles/spheres-cones-cylinders#sphere-maps.
Codificación de sistemas de referencia¶
Existe una gran cantidad de sistemas de referencia, por lo que se hace necesaria una forma de organizarlos.
El European Petroleum Survey Group recopiló una base de datos, ahora llamada EPSG Geodetic Parameter Dataset, con una colección de definiciones de sistemas de referencia de coordenadas y de transformaciones entre sistemas globales, regionales, nacionales y locales. En la actualidad, esta base de datos es mantenida por el Comité de Geomática de la International Association of Oil & Gas Producers.
Cada sistema de referencia de coordenadas cuenta con un código, llamado código EPSG. Algunos código EPSG son:
Código EPSG |
Sistema de referencia |
Observaciones |
|---|---|---|
WGS 84 – WGS84 - World Geodetic System 1984 |
Utilizado en dispositivos GPS |
|
WGS 84 / Pseudo-Mercator – Spherical Mercator |
Creado por Google a principios 2005 para Google Maps, es utilizado también por otros principales servicios de cartografía por Internet: OpenStreetMap, Bing Maps y otros. A veces es referenciado como 900913 (denominado así inicialmente y de manera no oficial por el proyecto OpenLayers) |
|
CR05 / CRTM05 |
Sistema oficial de Costa Rica |
|
WGS 84 / UTM zone 16N |
UTM para Costa Rica |
|
WGS 84 / UTM zone 17N |
UTM para Costa Rica |
|
Ocotepeque 1935 / Costa Rica Norte |
Proyección Lambert para Costa Rica norte |
|
Ocotepeque 1935 / Costa Rica Sur |
Proyección Lambert para Costa Rica sur |
La base de datos EPSG puede consultarse en http://epsg.io/.
Ejemplos de mapas¶
El uso de los conceptos cartográficos y geodésicos estudiados en este capítulo se ilustra en la Fig. 13.
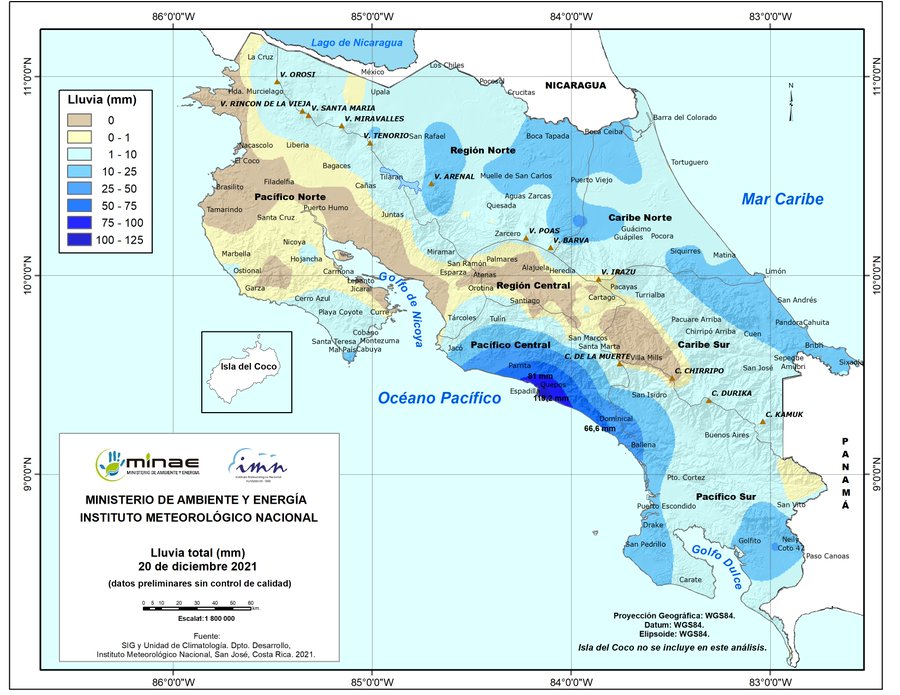
Fig. 13 Mapa de lluvia en Costa Rica. Fuente: Instituto Meteorológico Nacional (IMN).¶